Occluding Contour Breakthroughs, Part 1: A Surprisingly Hard Problem
This blog post has now been revised and adapted into a paper. Please cite the paper where appropriate:
- A. Hertzmann, “New Insights in Smooth Occluding Contours for Nonphotorealistic Rendering” in IEEE Computer Graphics and Applications, vol. 44, no. 01, pp. 76-85, 2024. [Paper (open access)]
The occluding contours of a smooth surface let you render 3D objects in many different artistic styles, such as this pen-and-ink hatching style:

Simple occluding contour renderings appear throughout many kinds of animations, TV shows and films throughout the past few decades, often consisting of basic black outlines. Some recent examples include the game “Hi-Fi Rush” and the Spider-Verse movies:

Now, there are a lot richer classes of stylizations in the research literature. Here are some examples:
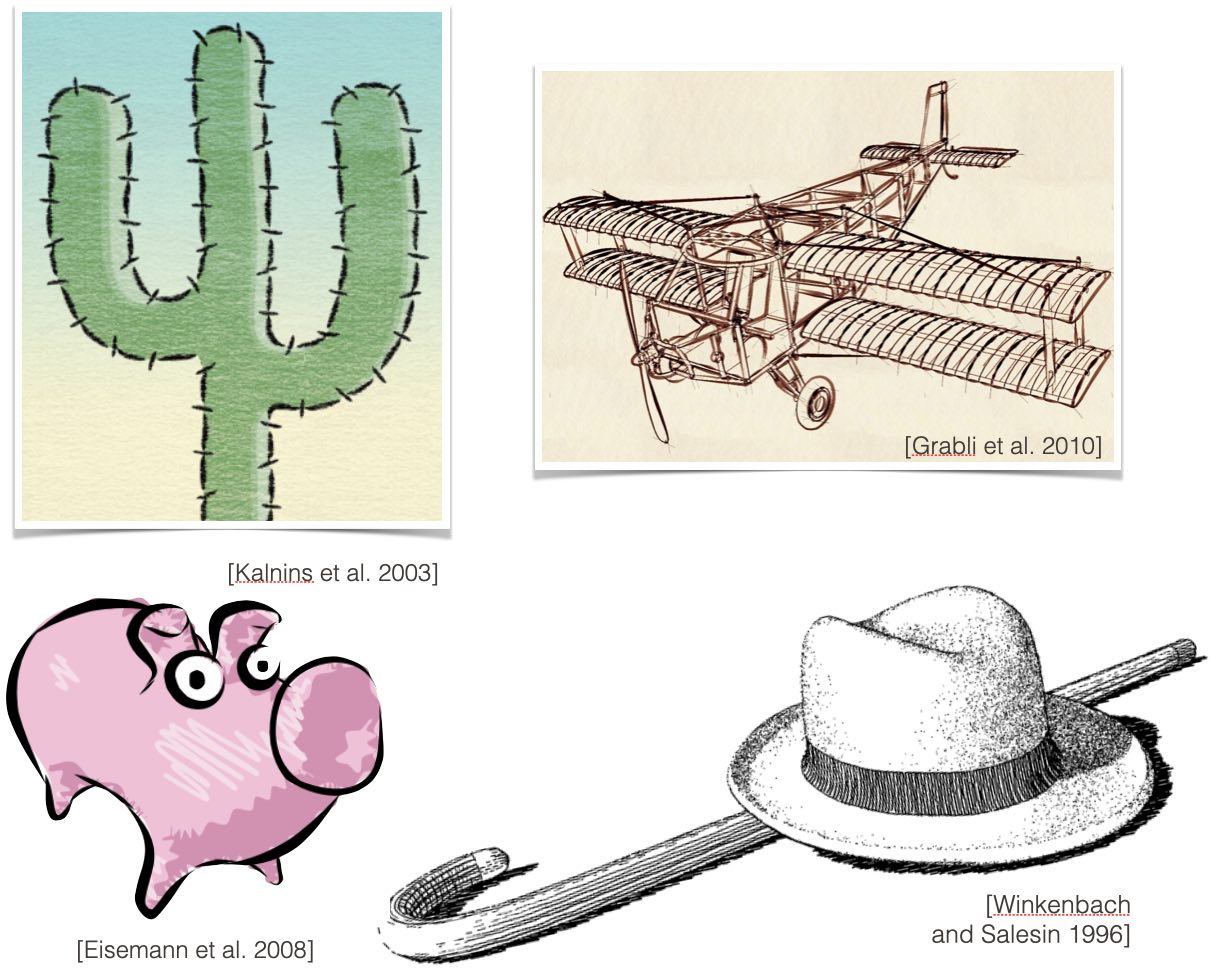
But we’re not seeing these styles in games or movies. Why not? These styles rely on vector contour extraction algorithms, and all of the existing algorithms for smooth surfaces have unpredictable failure cases. And we’ve never really understood why.
This year, we finally cracked the case.
In a paper called ConTesse, we finally explain exactly what the problem really is, and describe when a solution works or doesn’t; moreover, we describe a method that produces correct results for subdivision surfaces. And, in a second paper, we show how to generate exact smooth contours based on input meshes, allowing for very fast and accurate contours.
In this blog post, I explain exactly what the problem is, and, in the next post, what the breakthroughs are. In the third post, I recommend which of the existing methods to try for different types of problems, and point to where more research and development is needed to move these ideas from research to practical applications.
This post is intended for readers knowledgable about computer graphics algorithms. You can find a non-technical introduction to these topics here.
The Occluding Contour Problem
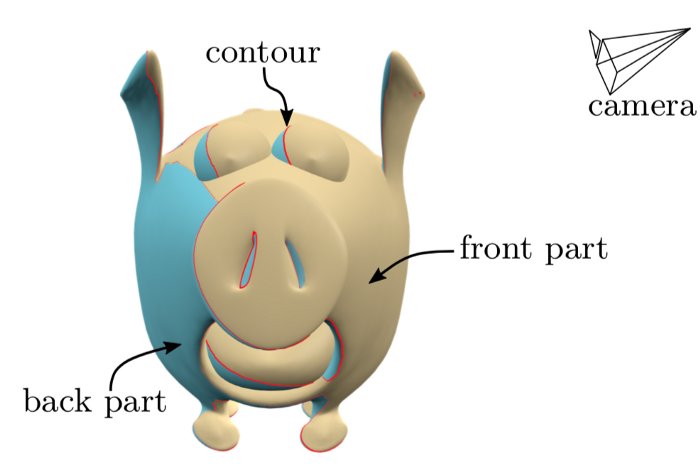
Here’s an example of occluding contours, drawn as black lines on a 3D model:

The occluding contours occur where a surface overlaps itself in image space:
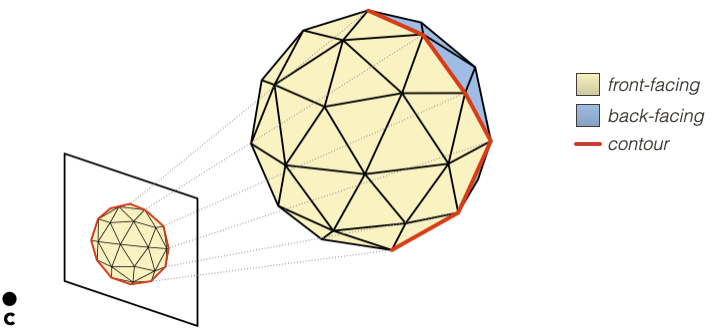
For a triangle mesh, it’s easy to find the occluding contours: take all the edges that connect a front-face to a back-face, and then compute which of those edges are visible:
Our existing algorithms for triangle mesh contours are robust and effective.
I’m assuming that the surface is oriented: the faces have normal directions consistent with their neighbors, and the camera position is constrained, so that only front-facing surface will ever be visible. These assumptions are common in computer graphics applications.
(In this post, I am being very casual with definitions and terminology. You can see our tutorial paper for a detailed and precise definitions.)
For smooth surfaces, i.e., surfaces with continous normals, the occluding contours are all visible surface points where the tangent plane contains the view vector. For example:
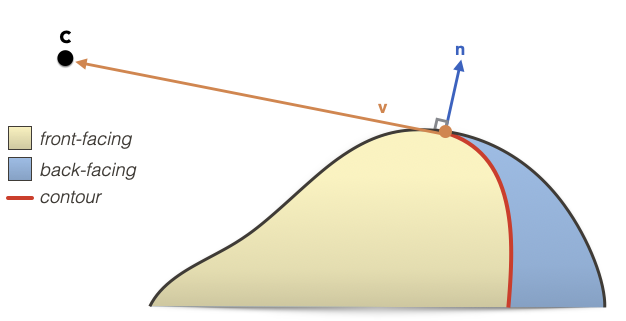
That shouldn’t be so hard to compute, right?
Topology Problems
What makes the problem difficult isn’t computing the contour points, it’s computing the visible points. We want the visible curves to have sensible topology: no gaps at all in the outlines, nor extra curves and junctions, or other mistakes that would mess up stylization.
For example, suppose you start with this smooth object:
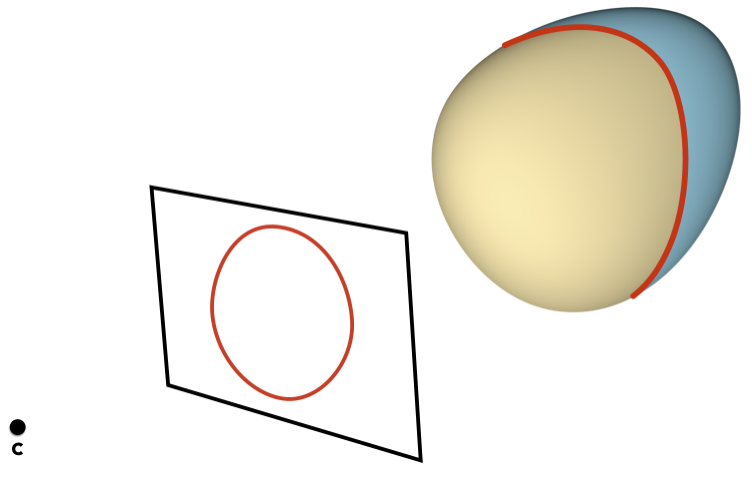
The obvious thing is to triangulate it into a mesh, and then compute the contours of the mesh. But look what happens:
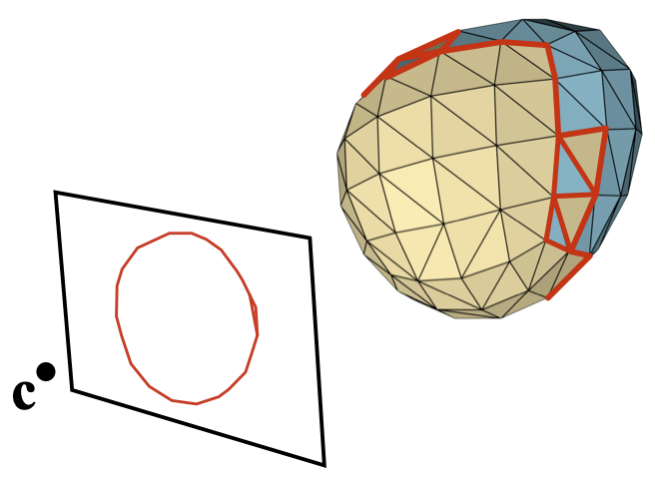
The smooth object has a simple contour, but the triangle mesh’s contour has lots of extra complicated pieces. This is because the surface is no longer cleanly split into one front-facing region and one back-facing region. The simple contour has become a mess, and this gets worse as surfaces get more complicated:

(This is an older rendering with a different color scheme for front and back faces.)
This matters when you try to stylize the contours, such as this animation:
Note how the stylization flickers and strokes appear and disappear, despite a number of attempts in this algorithm to keep things coherent.
Really, It’s Shockingly Hard
If you are like most researchers, you might think there are simple solutions to this problem. In my experience, pretty much everyone, when confronted with these problems, immediately suggests simple solutions that they confidently believe will solve the problem.
For example, you could come up with simple rules to fix up the curves, but these will all fail in various ways. You could try subdividing the surface (as did one very confident paper reviewer recently told us), but this doesn’t fix anything (we analyzed why in our 2014 paper). Nothing has worked robustly. Many other algorithms are surveyed in our tutorial paper, Chapters 6 and 7.
We proposed one of these algorithms in our 2001 paper, an interpolation-based approach that makes nice smooth curves. But, if you zoom in on the figures, you can see gaps in the outlines:
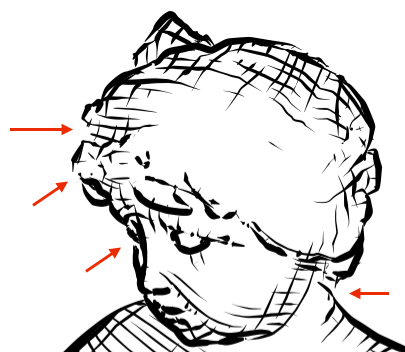
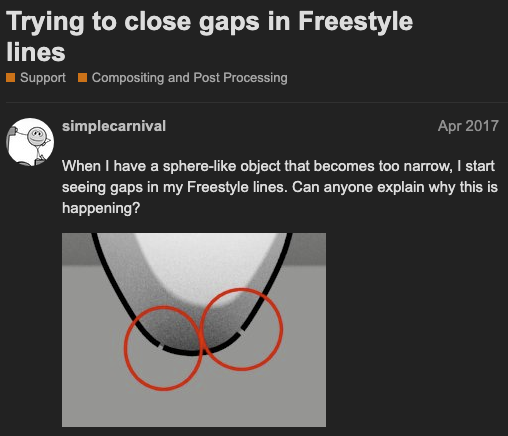
And this affects real applications. For example, Blender Freestyle uses our 2001 algorithm, from the implementation in Stephane Grabli’s work. Online, you can find many complaints about the gaps in Freestyle’s contours:
And, here’s an animation from a 2011 paper that tries to fix our method using planar maps, but still has gaps in the outline in some frames:
Even the pig image, which we showed in our survey paper, has an incorrect gap that I only just noticed writing this post.
In addition to their effects on animation, gaps and other errors prevent vectorization, converting these curves to 2D vector graphics. This is important for region-based stylization, filling regions with styles, since style is not just about outline curves, it’s about how you fill in regions as well.
This problem was first published in 1966; it’s older than photorealistic computer graphics. Depending on how you count, I’ve spent nearly a decade of my career working on this one little problem (that’s wall-clock time, not system time). You try implementing something, and it seems like there’s just one or two cases to fix with heuristics, but then other cases don’t work… and it becomes whack-a-mole. Nothing works reliably.
And it wasn’t just that we didn’t know how to get the curves looking “right”, we didn’t even know how, exactly, to define the problem… what does “right” even mean here?